Recherche du taux d'apprentissage avec lr

library(luz)
library(torch)
library(torchvision)
set.seed(1)
torch::torch_manual_seed(1703)

Dans cet article, nous allons discutiscuter de comment trouver un bon taux d’apprentissage pour votre modèle. Trouver un bon taux d’apprentissage est essentiel pour l’apprentissage optimal de votre modèle : Si il est trop faible, vous aurez besoin de trop d’itérations pour que votre fonction de coût converge, et cela pourrait être inutilisable si votre modèle prend trop de temps à ajuster. Si il est trop élevé, la fonction de coût peut exploser et vous aurez échoué à minimiser la perte.

Le taux d’apprentissage est parfois considéré comme un des hyper-paramètres de votre modèle comme les autres qui nécessite une optimisation, mais en réalité, il existe des techniques qui permettent de sélectionner un bon taux d’apprentissage pour votre modèle sans avoir à utiliser la stratégie coûteuse consistant à multiplier les modèles à ajuster avec différents taux d’apprentissages et en choisissant le meilleur à la fin.

Cet article de Leslie Smith, qui est devenu populaire après que son approche a été mise en œuvre dans la plateforme FastAI, propose de commencer avec un taux d’apprentissage très faible et le faire augmenter progressivement jusqu’à un taux d’apprentissage trop élevé. À chaque itération on enregistre la valeur de la perte et on visualise cette perte en fonction du taux d’apprentissage. On peut alors utiliser ces résultats pour décider d’un bon taux d’apprentissage. C’est ce que fait lr_finder, et nous allons voir comment l’utiliser.

Tout d’abord, téléchargeons et préparons les données de MNIST :

dir <- "~/Downloads/mnist" # répertoire de cache

train_ds <- mnist_dataset(
  dir,
  download = TRUE,
  transform = transform_to_tensor
)

On va ensuite définir notre réseau. On va utiliser un petit CNN dans le style LeNet.

net <- nn_module(
  "net",
  initialize = function() {
    self$features <- nn_sequential(
      nn_conv2d(1, 32, 3, 1),
      nn_relu(),
      nn_max_pool2d(2),
      nn_conv2d(32, 64, 3, 1),
      nn_relu(),
      nn_max_pool2d(2),
      nn_dropout(0.1),
      nn_flatten()
    )
    self$classifier <- nn_sequential(
      nn_linear(1600, 128),
      nn_dropout(0.1),
      nn_linear(128, 10)
    )
  },
  forward = function(x) {
    x %>% 
      self$features() %>% 
      self$classifier()
  }
)

On peut maintenant utiliser la fonction lr_finder pour enregistrer la perte avec différents taux d’apprentissages. Il est important d’utiliser la recherche de taux d’apprentissage avec tous les autres hyper-paramètres du modèle fixés, car ils peuvent influencer le choix du taux d’apprentissage. Par exemple, la taille des lots va vous conduire à différents taux d’apprentissages.

model <- net %>% setup(
  loss = torch::nn_cross_entropy_loss(),
  optimizer = torch::optim_adam
)

records <- lr_finder(
  object = model, 
  data = train_ds, 
  verbose = FALSE,
  dataloader_options = list(batch_size = 32),
  start_lr = 1e-6, # la plus petite valeur qui sera essayée
  end_lr = 1 # la plus grande valeur à essayer
)

str(records)
#> Classes 'lr_records' and 'data.frame':   100 obs. of  2 variables:
#>  $ lr  : num  1.15e-06 1.32e-06 1.51e-06 1.74e-06 2.00e-06 ...
#>  $ loss: num  2.31 2.3 2.29 2.3 2.31 ...

Le résultat est un tableau de données avec les pertes et le taux d’apprentissage à chaque étape. Vous pouvez utiliser la méthode de visualisation intégrée pour afficher les résultats exacts, ainsi qu’une valeur de perte lissée exponentiellement.

plot(records) +
  ggplot2::coord_cartesian(ylim = c(NA, 5))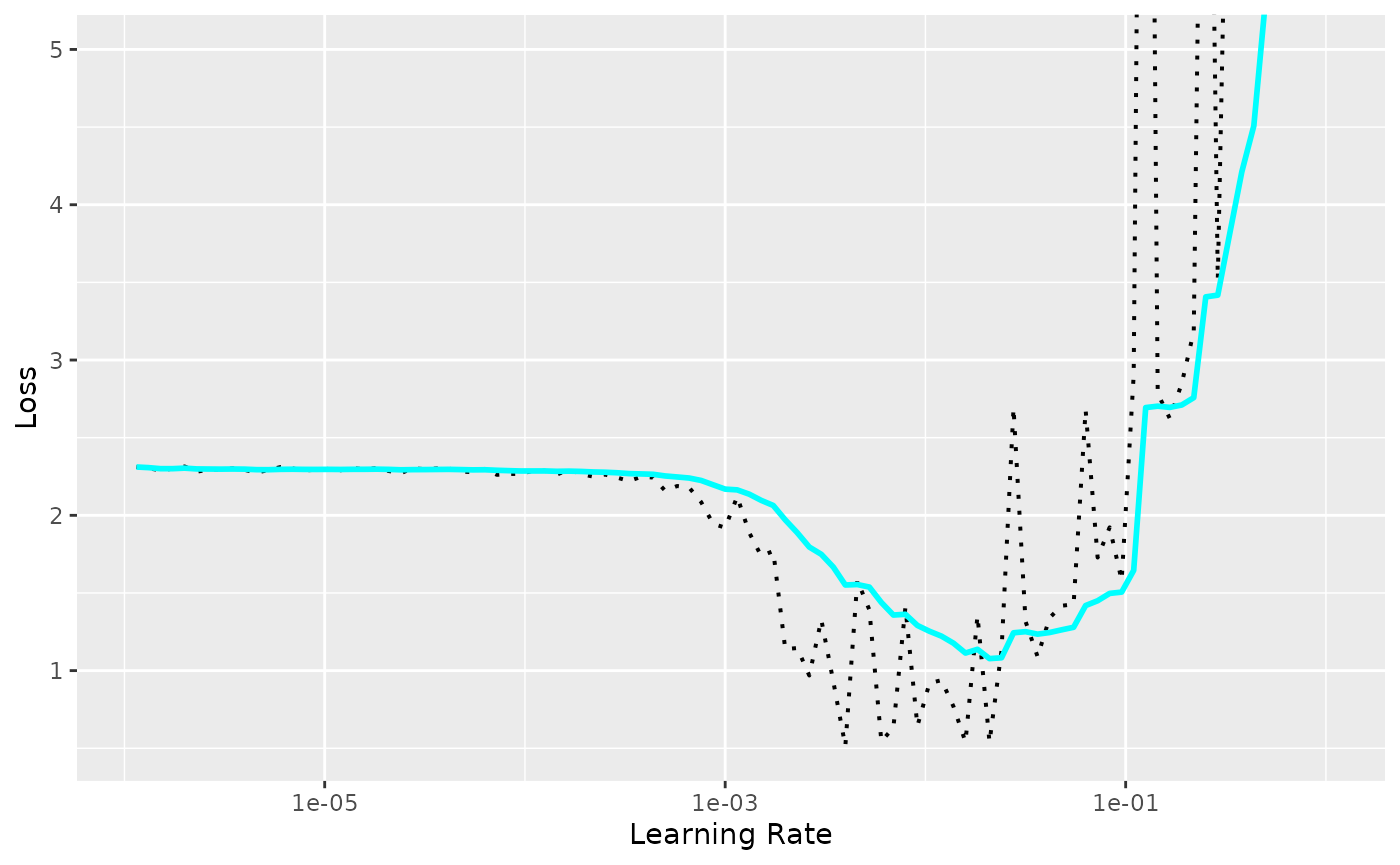

On peut voir que pour des taux d’apprentissage faibles la perte ne diminue pas. À partir d’un certain point, la perte commence à diminuer jusqu’à atteindre un point où elle commence à augmenter et enfin à exploser.

Et comment choisit-on le taux d’apprentissage à partir de cette courbe? Sylvain Gugger s’est posé la question dans cet article et y répond. En voici la traduction :

On ne choisit pas le taux d’apprentissage correspondant au minimum. Pourquoi ? Eh bien, le taux d’apprentissage qui correspond à la valeur minimale est déjà un peu trop élevé, car nous sommes, avec cette valeur, à la limite entre l’amélioration et l’explosion totale. Nous choisirons la valeur un ordre de grandeur en dessous, une valeur qui restera agressive (pour qu’on apprenne vite) mais toujours en retrait par rapport à l’explosion.

Ainsi, dans notre exemple, on choisira $10^{-3}$ au lieu de $10^{-2}$ . On peut maintenant fixer le taux d’apprentissage ainsi choisi dans notre modèle principal et conduire une optimisation des autres hyper-paramètres pour obtenir un bon score et minimiser au mieux la fonction de perte.

Recherche du taux d'apprentissage avec lr_finder